Patrick Naylor

I'm an Assistant Professor in the Department of Mathematics & Statistics at McMaster University. Previously, I was an NSERC Postdoctoral Fellow at Princeton University, and I completed my PhD at the University of Waterloo under the supervision of Doug Park.My research interests are in low-dimensional and geometric topology. My non-research interests include running, cycling, and drinking too much coffee.You can find more information about my 3D printing interests under Printing.

(Above: the model of a 120-cell currently hanging in the M3 atrium at UW)

Research

I study geometric and low-dimensional topology in dimensions 3 and 4. Questions about 4-manifolds are particularly interesting because of exotic phenomena: objects which are topologically equivalent but smoothly distinct. Most of my work has been constructive, i.e., about producing diffeomorphisms, or proving that certain objects are smoothly equivalent.Image: an interactive 3D model of the Stevedore knot, a nontrivial slice knot.

Publications and preprints

Exotic definite four-manifolds with non-cyclic fundamental group (with Robert Harris and B. Doug Park). Submitted. [arXiv].
Doubling Gluck twists: a 5-dimensional approach (with David Gabai and Hannah Schwartz). Submitted. [arXiv].
Negacylic weighing matrices (with Robert Craigen, Colin Desmarais, and Ted Eaton). Submitted.
Multisections of 4-manifolds (with Gabriel Islambouli). To appear in the Transactions of the American Mathematical Society. [arXiv].
Trisections of non-orientable 4-manifolds (with Maggie Miller). To appear in the Michigan Mathematical Journal. [DOI], [arXiv].
Trisection diagrams and twists of 4-manifolds. Comptes Rendus Mathématique 360:845–866, 2022. [DOI], [arXiv].
Gluck twisting roll spun knots (with Hannah Schwartz) Algebraic & Geometric Topology 22(2), 973–990, 2022. [DOI], [arXiv].
From automorphisms of Riemann surfaces to smooth 4-manifolds (with Ahmet Beyaz, Sinem Onaran, and B. Doug Park). Math Res. Lett. 27(3), 629-645, 2020. [DOI].
Testing bi-orderability of knot groups (with Adam Clay and Colin Desmarais) Canad. Math. Bull. 59(3), 472-482, 2016. [DOI], [arXiv].

Teaching

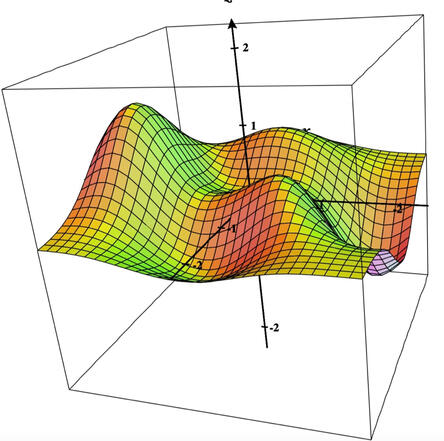
In Winter 2025, I'm teaching MATH 2XX3: Advanced Calculus II. More information can be found on Avenue.Image: the graph of a function, produced using CalcPlot3D.

In Spring 2023, I taught MAT 203: Advanced Vector Calculus at Princeton University. I produced a variety of 3D-printed models for the course using a combination of OpenSCAD, CalcPlot3D and Blender/Cura. For more information on 3D printing for mathematics education, see the page on Printing.In Spring 2020, I taught Math 235 at the University of Waterloo. I produced a few videos that you may find useful: you can find them here.

Outreach

I have been a presenter for Math Circles, an after-school mathematics enrichment program for high school students run by the Center for Education in Mathematics and Computing (CEMC). If you're interested, links to some of my worksheets are below.

Mathematical Games: [Games 1], [Games 2], [Games 3], [Notes]
More Mathematical Games: [More Games], [Partitions], [Dwellings], [Solutions]
Knot theory: [Lesson], [Problems], [Solutions]

I love math contests, and have been involved in designing and marking some of the national contests that the CEMC has to offer.I have been a mentor for Camp Euclid, a 6 week mathematical research enrichment program for high school students run by David Gay at the University of Georgia.I also make high school visits to talk about mathematics and problem solving! If you're interested in having me visit your school, please get in touch.

3D Printing for Mathematics Education

In the summer of 2024, Caroline Junkins, Lee van Brussel and I ran an innovative project that combined 3D printing and math to enhance learning through accessibility. Our goals were for students to:

Gain hands-on experience with 3D printing technology,
Explore calculus concepts through practical application,
Contribute to making math education more accessible and inclusive.

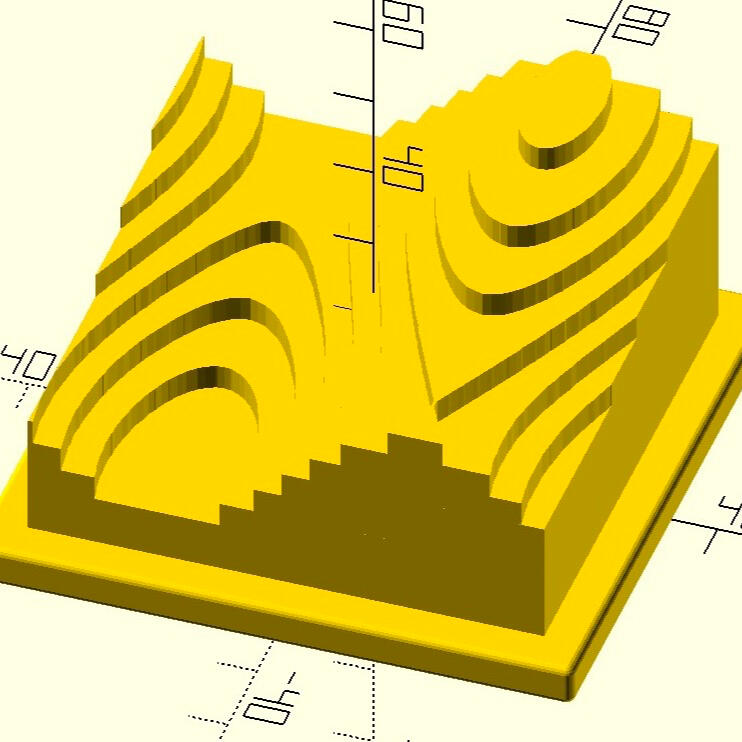
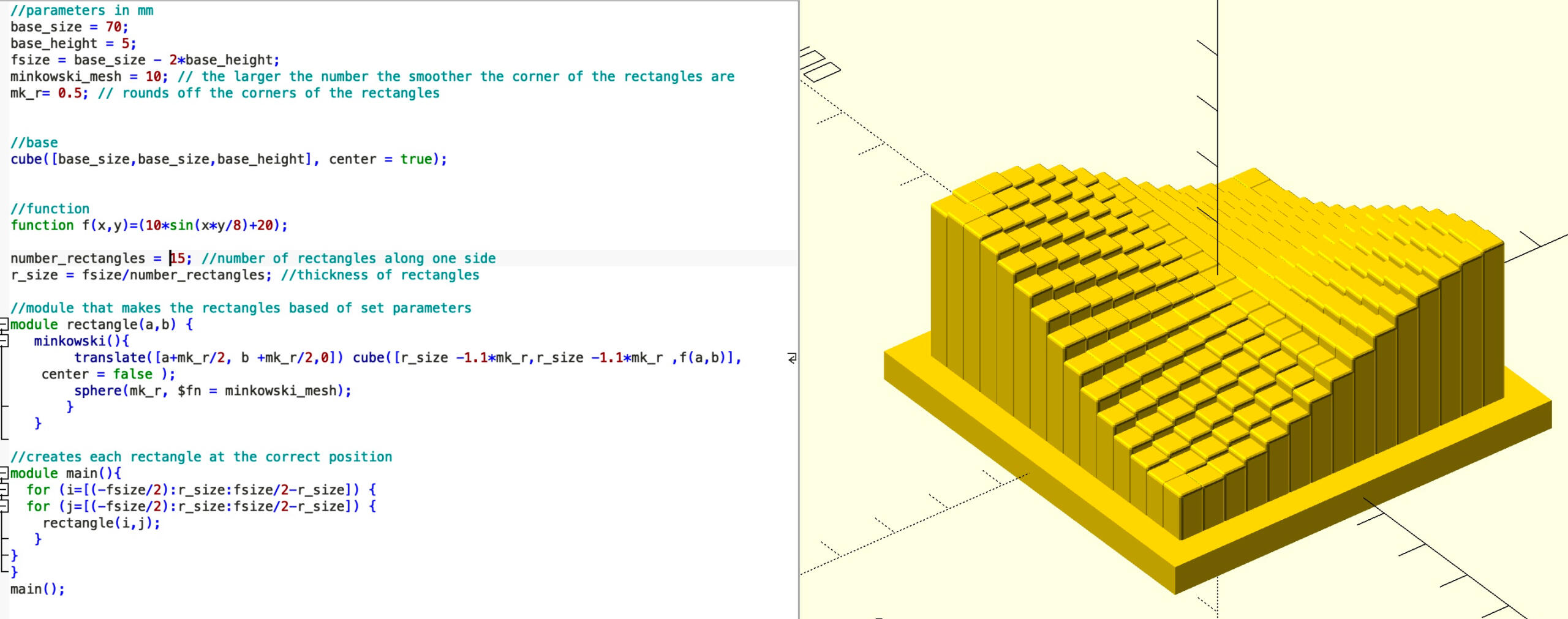
You can find a variety of pictures of models designed and produced by students using OpenSCAD. You can also read about this project in a Faculty of Science news article.Stay tuned for updates for Summer 2025!

Bonus: knots, links, and surfaces from MATH 4TT3/6TT3: Topics in Topology.

Seminars

This term, the Geometry & Topology seminar takes place on either Mondays or Thursdays at 3:30; upcoming talks can be found here.

Contact

The best way to contact me is by email, at:patrick.naylor@mcmaster.ca

319 Hamilton HallDepartment of Mathematics & Statistics
Hamilton Hall
1280 Main Street West
Hamilton, Ontario, L8S 4K1

I am currently looking for masters students to supervise. If you are interested in working with me, please contact me via e-mail. Applications from members of equity-deserving groups are especially welcome to apply.I am also looking for undergraduate summer research students, who are normally supported by an NSERC USRA. You can find more information here.

(Obligatory hiking photograph)

I am privileged to work at McMaster University, located on the traditional territories of the Mississauga and Haudenosaunee nations, and within the lands protected by the “Dish with One Spoon” wampum agreement.